INCREASING RETURNS
Self-Reinforcing Success
Networks have their own logic. When you connect all to all, curious things happen.
Mathematics says the sum value of a network increases as the square of the number of members. In other words, as the number of nodes in a network increases arithmetically, the value of the network increases exponentially.* Adding a few more members can dramatically increase the value for all members.
[*I use the vernacular meaning of “exponential” to mean “explosive compounded growth.” Technically, n2 growth should be called polynomial, or even more precisely, a quadractic; a fixed exponent (2 in this case) is applied to a growing number n. True exponential growth in mathematics entails a fixed number (say 2) that has a growing exponent, n, as in 2n. The curves of some polynomials and exponentials look similar, except the exponential is even steeper; in common discourse the two are lumped together.]
This amazing boom is not hard to visualize. Take 4 acquaintances; there are 12 distinct one-to-one friendships among them. If we add a fifth friend to the group, the friendship network increases to 20 different relations; 6 friends makes 30 connections; 7 makes 42. As the number of members goes beyond 10, the total number of relationships among the friends escalates rapidly. When the number of people (n) involved is large, the total number of connections can be approximated as simply n X n, or n2. Thus a thousand members can have a million friendships.
The magic of n2 is that when you annex one more new member, you add many more connections; you get more value than you add. That’s not true in the industrial world. Say you owned a milk factory, and you had 10 customers who bought milk once a day. If you increased your customer base by 10% by adding one new customer, you could expect an increase in milk sales of 10%. That’s linear. But say, instead, you owned a telephone network with 10 customers who talked to each other once a day. Your customers would make about n2 (102), or 100 calls a day. If you added one more new customer, you increased your customer base by 10%, but you increased your calling revenue by a whopping 20% (since 112 is 20% larger than 102). In a network economy, small efforts can lead to large results.
INCREASING RETURNS
A network’s tendency to explode in value mathematically
was first noticed by Bob Metcalfe, the inventor of a localized networking technology called Ethernet. During the late 1970s Metcalfe was selling a combination of Ethernet, Unix, and TCP/IP (the internet protocol), as a way to make large networks out of many small ones. Metcalfe says, “The idea that the value of a network equals n squared came to me after I failed to get networks to work on a small scale, despite many repeated experiments.” He noticed that networks needed to achieve critical mass to make them worthwhile. But he also noticed that as he linked together small local networks here and there, the value of the combined large network would multiply abruptly. In 1980 he began formulating his law: value = n x n.
In fact, n2 underestimates the total value of network growth. As economic journalist John Browning notes, the power of a network multiplies even faster than this. Metcalfe’s observation was based on the idea of a phone network. Each telephone call had one person at each end; therefore the total number of potential calls was the grand sum of all possible pairings of people with phones. But online networks, like personal networks in real life, provide opportunities for complicated three-way, four-way, or many-way connections. You can not only interact with your friend Charlie, but with Alice and Bob and Charlie at the same time. The experience of communicating simultaneously with Charlie’s group in an online world is a distinct experience, separate in its essential qualities, from communicating with Charlie alone. Therefore, when we tally up the number of possible connections in a network we have to add up not only all the combinations in which members can be paired, but also all the possible groups as well. These additional combos send the total value of the network skyrocketing. The precise arithmetic is not important. It is enough to know that the worth of a network races ahead of its input.
This tendency of networks to drastically amplify small inputs leads to the second key axiom of network logic: the law of increasing returns. In one way or another this law undergirds much of the strange behavior in the network economy. The simplest version goes like this: The value of a network explodes as its membership increases, and then the value explosion sucks in yet more members, compounding the result.
INCREASING RETURNS
An old saying puts it succinctly: Them that’s got shall get.
A new way of saying it: Networks encourage the successful to be yet more successful. Economist Brian Arthur calls this effect “increasing returns.” “Increasing returns” he says, “are the tendency for that which is ahead to get further ahead; for that which loses advantage to lose further advantage.”
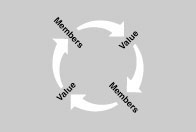
In networks, we find self-reinforcing virtuous circles. Each additional member increases the network’s value, which in turn attracts more members, initiating a spiral of benefits.
INCREASING RETURNS
In the industrial economy success was self-limiting;
…it obeyed the law of decreasing returns. In the network economy, success is self-reinforcing; it obeys the law of increasing returns.
We see the law of increasing returns operating in the way areas such as Silicon Valley grow; each successful new start-up attracts other start-ups, which in turn attract more capital and skills and yet more start-ups. (Silicon Valley and other high-tech industrial regions are themselves tightly coupled networks of talent, resources, and opportunities.)
At first glance the law of increasing returns may seem identical to the familiar textbook notion of economies of scale: The more of a product you make, the more efficient the process becomes. Henry Ford leveraged his success in selling automobiles to devise more productive methods of manufacturing cars. This enabled Ford to sell his cars more cheaply, which created larger sales, which fueled more innovation and even better production methods, sending his company to the top.
That self-feeding circle is a positive feedback loop. While the law of increasing returns and the economies of scale both rely on positive feedback loops, there are two key differences.
First, industrial economies of scale increase value gradually and linearly. Small efforts yield small results; large efforts give large results. Networks, on the other hand, increase value exponentially–small efforts reinforce one another so that results can quickly snowball into an avalanche. It’s the difference between a piggy bank and compounded interest.
Second, and more important, industrial economies of scale stem from the herculean efforts of a single organization to outpace the competition by creating value for less. The expertise (and advantage) developed by the leading company is its alone. By contrast, networked increasing returns are created and shared by the entire network. Many agents, users, and competitors together create the network’s value. Although the gains of increasing returns may be reaped unequally by one organization, the value of the gains resides in the greater web of relationships.
These positive feedback loops are created by “network externalities.” Anything that creates (or destroys) value which cannot be appointed to someone’s account ledgers is an externality. The total value of a telephone system lies outside the total internal value of the telephone companies and their assets. It lies externally in the greater phone network itself. Networks are particularly potent sources of external value and have become a hot spot of economic investigation in the last decade. A parade of recently published academic papers scrutinize the fine points of network externalities: When do they arise? How do they break down? Are they symmetrical? Can they be manipulated?
INCREASING RETURNS
One reason increasing returns and network externalities are garnering attention…
…is because they tend to create apparent monopolies. Huge amounts of cash pour toward network winners such as Cisco or Oracle or Microsoft, and that makes everyone else nervous. Are network superwinners in fact monopolies? They are not like any monopolies of the industrial age. When antitrust hearings are conducted today, the witnesses are not customers angered by high pricing, haughty service, or lack of options–the traditional sins of a monopolist. Customers have nothing to complain about because they get lower prices, better service, and more features from network superwinners–at least in the short term. The only ones complaining about superwinners are their competitors, because increasing returns create a winner-take-most environment. But in the long term, the customer will have reason to complain if competitors pull back or disappear.
The new monopolies are different in several ways. Traditional monopolies dominated commodities. In the new order, as Santa Fe Institute economist Brian Arthur points out, “Dominance may consist not so much in cornering a single product as in successively taking over more and more threads of the web of technology.” Superwinners can practice a type of crossover where control of one layer of the web leverages control into others. Owning the standard for voice phone calls can ease the likelihood of owning the standard for fax transmissions.
The unacceptable transgression of the traditional monopolist was that as a mono-seller (thus the Greek, mono-polist), it could push prices up and quality down. But the logic of the net inherently lowers prices and raises quality, even those of a single-seller monopolist. In the network economy, the unpardonable transgression is to stifle innovation, which is what happens when competition is stifled. In the new order, innovation is more important than price because price is a derivative of innovation.
INCREASING RETURNS
Mono-sellers are actually desirable…
…in a network economy. Because of increasing returns and n2 value, a single large pool is superior to many smaller pools. The network economy will breed mono-sellers with great fertility. What is intolerable in a network economy is “monovation”–depending upon a single source of innovation. The danger of monopolists in the network economy is not that they can raise prices but they can become monovationists. But there are ways to encourage “polyvation”–multiple sources of innovation–in a world of monopolists: by creating open systems, by moving key intellectual properties into the public domain, by releasing source code democratically. As we come to understand the importance of increasing returns and the other new rules of the network economy, we can expect shifts in our understanding of the role of market winners.
Industrial monopolies exploited simple economies of scale for their own benefit. Network effects are not about economies of scale, they are about value that is created above and beyond a single organization–by a larger network–and then returned to the parts, often unevenly. Because some portion of the value of a network firm so obviously comes from external sources, allegiance is often granted to external sources.
We see this in the way network effects govern the growth of Silicon Valley. Silicon Valley’s success is external to any particular company’s success, and so loyalty is external, too. As AnnaLee Saxenian, author of Regional Advantage, notes, Silicon Valley has in effect become one large, distributed company. People job-hop so frequently that folks “joke that you can change jobs without changing car pools. Some say they wake up thinking they work for Silicon Valley. Their loyalty is more to advancing technology or to the region than it is to any individual firm.”
This trend seems likely to extend further. We are headed into an era when both workers and consumers will feel more loyalty to a network than to any ordinary firm. The great innovation of Silicon Valley is not the wowie-zowie hardware and software it has invented. Silicon Valley’s greatest “product” is the social organization of its companies and, most important, the networked architecture of the region itself–the tangled web of former jobs, intimate colleagues, information leakage from one firm to the next, rapid company life cycles, and agile email culture. This social web, suffused into the warm hardware of jelly bean chips and copper neurons, creates a true network economy.
INCREASING RETURNS
The social web, even in the Valley…
…displays some stress marks. There is no question that the network economy is, at worst, winner-take-all, and at best, winner-take-most. The trajectory of increasing returns and a shortage of attention focuses success toward a few points. Stars and hits rise, while the rest languish. Mundane appliances and bulky objects now seem to follow the Hollywood model: A few brands sell like crazy, and the rest sell only a few. It’s a “hits” economy, where resources flow to those that show some life. If a new novel, new product, or new service begins to succeed it is fed more; if it falters, it’s left to wither. Them that has, gets more.
The current great debate is whether the law of increasing returns favors the early or not. In some of the first studies of increasing returns, economist Brian Arthur discovered that when technological competitors, such as the VHS and Betamax video formats, were modeled in a computer, increasing returns favored one technology over the other–to the eventual demise of the unfortunate one (in this case Betamax). And “unfortunate” is the right word. According to Arthur’s research, the technology that came to dominate, thanks to increasing returns, was not necessarily the superior one. It was just the lucky one. Or the early one. Arthur writes: “If a product or a company or a technology–one of many competing in a market–gets ahead by chance or clever strategy, increasing returns can magnify this advantage, and the product or company can go on to lock in the market.”
All things being equal, early success has a measurable advantage. But in real life all things are rarely equal. Technologies which seem to be inferior and yet prevail through the dynamics of increased returns often reveal themselves under further study to be slightly superior in key ways. The Sony Betamax format lost to VHS because it couldn’t record for as long as VHS could, and, according to some, because Sony discouraged Beta use for porno–an early use of video. Apple Computer’s superior operating system lost to Windows because Apple had an inferior price–due to its misguided monopolist strategy. The supposedly ergonomic Dvorak keyboard lost to the all-too-familiar QWERTY keyboard because the Dvorak layout really wasn’t any faster.
Being first or best sometimes helps, but not always. The outcome of competition in a network is not determined solely by the abilities of the competitors, but by tiny differences, including luck, that are greatly magnified by the power of positive feedback loops. The fate of competition is “path dependent” on minor nudges and hurdles that can “tip” the system in one direction or another. Final destiny cannot be predicted on the basis of exceptional attributes alone.
INCREASING RETURNS
What can be predicted…
…is the way in which networks enlarge small advantages, and then lock the advantage in. In the same way, initial parameters and conventions can quickly freeze into unalterable standards. The solidifying standards of a network are both a blessing and a curse–a blessing because the ad hoc agreement reduces risk, and thus sparks widespread progress, and a curse because those who own or control the standard are disproportionately rewarded.
But the network economy doesn’t allow the blessing without the curse. Microsoft’s billions are tolerated (more or less) because so many others in the network economy have made their collective billions on the advantages of Microsoft’s increasing-returns standards.
We forget how recent and sudden Microsoft’s prominence is. Microsoft is a textbook example of Metcalfe’s law (“The value of Windows increases exponentially as its users increase arithmetically”) and the law of increasing returns (“The more who use NT, the more attractive NT becomes”). Microsoft also illustrates the third corollary of increasing returns: how small signals can suddenly become booms.
INCREASING RETURNS
During its first 10 years…
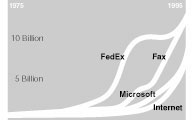
…Microsoft’s profits were negligible. Its profits rose above the background noise of Wall Street only around 1985. But once they began to rise, they exploded. A chart of Microsoft’s cornucopia of profits is an exponentially booming curve, one that parallels several other rising stars in the network economy.
Federal Express experienced a similar trajectory: years of minuscule profit increases, slowly ramping up to an invisible threshold, and then surging skyward in a blast sometime during the early 1980s.
The story of fax machines is likewise a tale of a 20-year-long overnight success. After two decades of marginal success, the number of fax machines quietly crossed the point of no return during the mid-1980s–and the next thing you know, they were everywhere.
Network organizations experience small gains while thieir network is being seeded. Once the network is established, explosive growth follows with relatively little additional genius.
The archetypal case of a success explosion in a network economy is the internet itself. As any proud old-time nethead will be happy to explain, the internet was a lonely (but thrilling!) cultural backwater for two decades before it showed up on the media radar. A graph of the number of internet hosts worldwide, starting in the 1970s, stays barely above the bottom line, until around 1991, when the global tally of hosts suddenly mushroomed, exponentially acting upward to take over the world.
The curves of Microsoft, the internet, fax machines and FedEx (I owe Net Gain author John Hagel credit for these four examples) are templates of exponential growth, compounding in a biological way. Such curves are almost the definition of a biological system. That’s one reason the network economy is often described most accurately in biological terms. Indeed, if the web feels like a frontier, it’s because for the first time in history we are witnessing biological growth in technological systems.
INCREASING RETURNS
A good definition of a network…
…is organic behavior in a technological matrix.
The compounded successes of Microsoft, FedEx, fax machines, and the internet all hinge on the prime law of networks: Value explodes exponentially with membership, and this heightened value acts like gravity drawing in yet more members. The virtuous circle inflates until all potential members are joined.
This explosion, however, did not ignite until approximately the late 1980s. Two things happened then–the dual big bangs of almost-free jelly bean chips and collapsing telco charges. It became feasible–that is, dirt cheap–to exchange data almost anywhere, anytime. The net, the grand net, began to precipitate out of this supersaturated solution. Network power followed.
One of the hallmarks of the industrial age was its reasonable expectations. Success was in proportion to effort. Small effort, small gains. Large effort, large gains. This linear ratio is typical of capital investments and resource allotments. According to data from the U.S. Statistical Abstract, the best-selling products in the 1950s–appliances such as refrigerators, clocks and washing machines–sold steadily with only a slight 2% annual increase in the number of units sold per year. To imagine the future of an enterprise or innovation one needed only to extrapolate the current trends in a straight line. There was a comfortable assumption–largely true–that the world proceeded linearly. Entirely new phenomenona did not ordinarily appear out of nowhere and change everything within months.
With the advent of large-scale electronic media networks in the mid century, that assumption began to erode. Millions of kids watching TV grew up to create rapid fads (hula hoops), instant youth cultures such as the beats and hippies, with sudden spontaneous gatherings of half a million, as at Woodstock. Events did not happen linearly. With media networks it was no longer safe to extrapolate the future from the recent past. When success came, it often fed on itself in crazy hyperkinetic booms. The recent sales of electronic pets is one example. Tamagotchis, the original brand of Japanese toy pets, went from sales of zero in Japan to 10 million units in their first year, to 20 million by the second year. When they were introduced in the United States a half million units were sold in the first month. The Tamagotchis could be actual breeding animals judging simply from their growth rate because their sales curve follows the population curve of reproducing biological animals. One day there are two pets, the next year there are 200. In biological populations, success can easily compound into runaway growth; now this wild runaway growth is happening with technology.

