Adaptive Basins and Strange Peaks
Biologists talk about adaptive landscapes. In these metaphorical places, species climb uphill towards optimal fitness. Going up is a struggle. Climbing takes energy. Optimal peaks can be hard to attain. Many species are distracted by getting stuck on sub-optimal false peaks, or waylaid by the intervening rugged landscape.
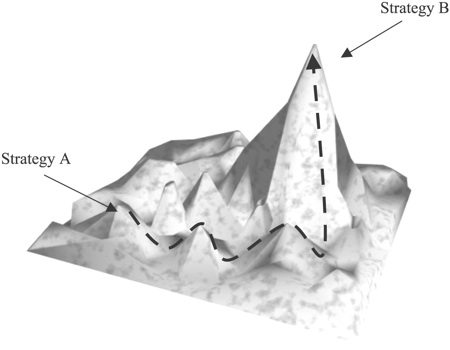
In this standard picture, the form of the peaks is created by the environment – say, the high peaks of fitness needed to survive in a desert. But of course, in real life, optimal fitness is a moving target, or a moving peak so to speak, that is formed in part by other organisms and by variation and behavior of the current organism itself. This is the view of co-evolution. In the new picture, constraints and self-organization can shape peaks, too. Either way, reaching an apex is the key effort.
But on the other side of science, in physics, the landscapes are inverted. Here physicists talk about basins in the landscape of thermodynamics. Strange attractors create deep wells that suck down entities. Getting out of the well is a struggle. Reversing out of the inverted peak is what takes energy. Reaching the bottom is the key effort.
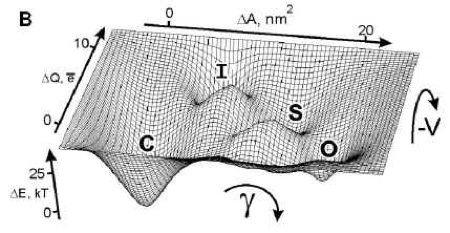
I suggest the at times the same forces which create peaks in evolutionary landscapes can also be thought of as wells, and we might better understand the path of a species in time not as an uphill climb onto an adaptive peak but a downhill fall into an adaptive well. An optimal form may sometimes work like a tractor-beam that pulls in an entity and keeps it there for a duration despite disruptions. Only a severe hit of energy and outside perturbations can dislodge it from a well and move into another form-basin.
This inverted view might illuminate inevitabilities as wells that complex structures fall into.


